在开发中有整数有浮点数的计算，对于浮点数计算往往会有些意想不到的结果
1
2
3
//js
>0.3+0.6
>0.8999999999999999
这个结果竟然不是0.9，那么为什么会出现这种情况，本文就针对于浮点数计算出现的”异常“进行说明。
浮点数分单精度(32bit)和双精度(64bit),两者基本概念都是一样的，为了方便讲解，就用单精度浮点数来进行说明。
浮点数的格式
我们先先看下单精度浮点数在计算机中如何定义格式的:
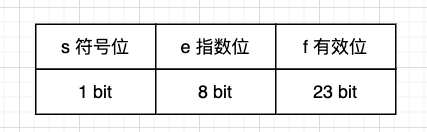
- 符号位：表示当前符号正负数，1：负数，0：正数。
- 指数位：表示2的幂次方，2^8 = 256表示0~255的正数范围，由于浮点数要表示正负，所以取范围为-126~127，浮点数不仅能表示很大的数也能表示很小的数。
- 有效位：表示浮点数二进制有效的长度，32位下有效位是23个bit。 综合科学计数法，浮点数表示如下：
任何浮点数都是对应一个二进制的表示，转换成二进制然后通过s+e+f的组合。会用几个例子进行说明。
浮点数的十进制转换二进制
举例数字：9.1
浮点数中小数点前后的计算方式是不同的，我们先对小数点前面的数字进行二进制转换，整数位的二进制转换使用的是除法取余数，
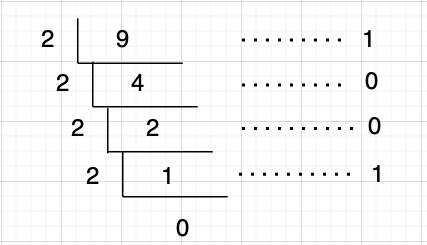
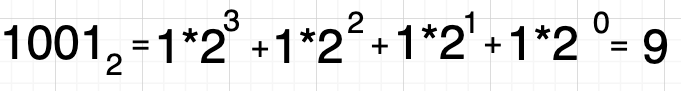
最后的结果是9 = 1001
然后对小数点后面数字进行二进制转换，小数部分转换二进制的方式跟整数正好相反，使用的是乘法，规则如下
- 使用小数位乘以2进行计算。
- 如果乘法计算后整数位为0，则二进制标记为0，继续进行乘法计算，直到小数位为0。
- 如果乘法计算后整数位为1，则二进制标记为1，整数位减去1继续进行乘法计算，直到小数位为0。
- 如果乘法出现无限循环则 只需到计算到有效位即可。
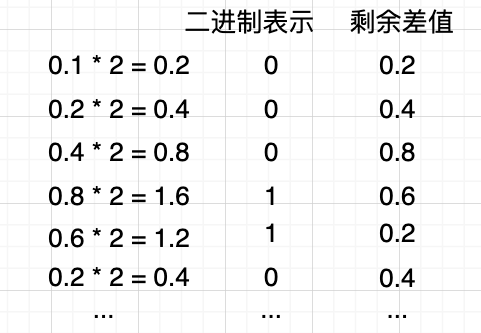注意这是个无限循环了。
最后把整数位和小数位结合下 ` 1,001.000,110,011,00….`
浮点数是由二进制的科学计数法来表示的，所以需要先把小数点左移三位,移动的位数作为指数位3(左移动为正，右移动为负)
1.001,000,110,011,00....
这样二进制表示法就写好了，不过还没有完成，记得上面那个公式吧，现在我们继续处理
先是有效位，有效位的长度是23bit，所以从小数点后数到第23位截止，后面多余的给截断，最终表示为001,000,110,011,001,100,110,01。
然后是指数位，前面已经知道指数位就是3了，由于指数位取值范围是-126~127，所以3在里面是130，130对应到二进制就是10000010
符号位最简单，因为是正数，所以就是0
最后将结果拼接起来就是9.1对应的二进制数：
0 10000010 00100011001100110011001
浮点数的二进制转十进制
刚刚把十进制的浮点数转换成了二进制，现在我再看看如何把二进制的浮点数给转换回去。通过结果会发现更多的问题，我们就先往下看吧。
0 10000010 00100011001100110011001
首先把9.1的二进制截取第一个bit符号位表示这个浮点数是正还是负。
10000010 00100011001100110011001
其次截取8bit指数位转换为十进制130，再根据浮点数范围计算出指数为3。
00100011001100110011001
根据指数位3 再截取3bit位(注意指数的正负)，得到001并且前面加1最终整数位是1001也就是9（如果想不明白可以参考十进制转二进制）
00011001100110011001
剩下的就是小数位的处理了，他计算的方式是小数点后开始第一个数乘以2的-1次方，以此类推。
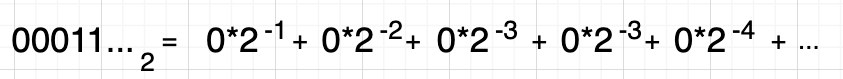
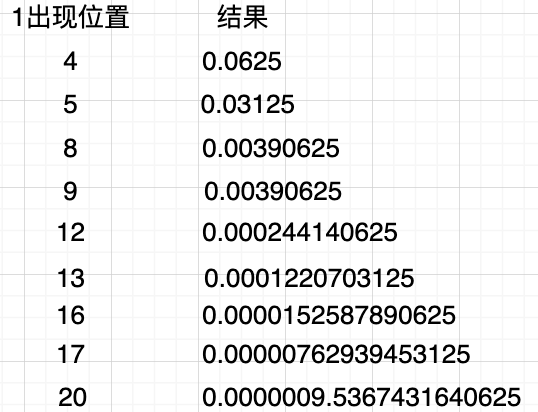已经为你们计算好1所在位置的值了，把这些数字和整数位加起来结果是9.099999427....,它最终结果并不是直接9.1，而是要经过四舍五入后近似等于。这个也间接说明文章开头0.3+0.6不等于0.9的问题了。
实际上浮点数能正确表示的数字也就0.5，0.25…等，其他的数表示基本上就是近似表示法。
附上一个连接,可以很直观的看到符号位，指数位和有效位的操作，每个bit的变化都会带来其他位置的变动。
浮点数加法计算
浮点数的加法计算的步骤是符号位先对其,有效位再计算
比如0.5+0.125进行浮点数计算，通过上面提供的工具 我们分别来看0.5和0.125对应的二进制数
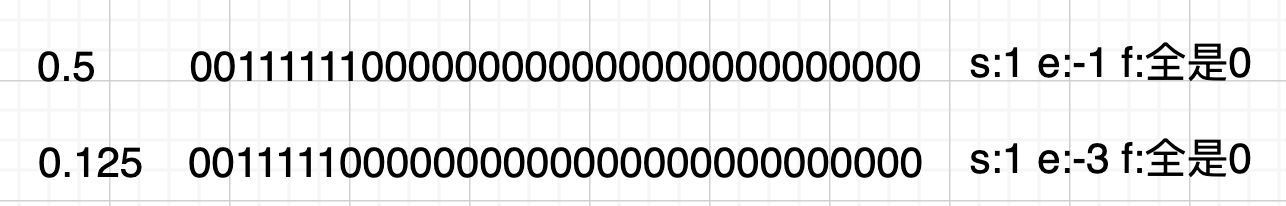
先说下有效位，0.5下 0.1000… 0.125下 0.00100… 遵循$ (-1)^{s} * 1.f * 2^{e} $，则0.5的二进制浮点数右移动1位为1.0000…，0.125的二进制浮点数下右移动(指数位为负数右移动)3位1.00000…
由于在加法计算中 先要将其符号位(往数字大的对齐)进行对齐， 则0.125对应二进制的指数位要变为-1，对应的有效位要由原本的0.001000 变为0.010000….
将两个有效位相加 1.010000….+ 0.01000… = 1.010000.. 在加上前面符号位和指数位(指数已经统为一1)为00111111001000000000000000000000，得出对应十进制数是0.625。
在浮点数加法中，指数位数字越小，它的有效位进行右移，在移动的过程中有效位可能会被逐渐丢弃，如果两个浮点数相差过大，在求和时候，较小的那个浮点数会发生精度丢失，位移越大，可能丢失的精度也就越大。 32位浮点数的有效位长度一共只有23位，如果两个数的指数位差出23位，较小的数右移24位之后，所有的有效位就都丢失了比如200万元和1元相加，最后那个1元就会被丢失掉。
